Fractal Flow is my largest programming project so far; here’s a little about it:
Early days
I started Fractal Flow on January 12th 2022, after a few months of learning and tinkering with the Windows Presentation Foundation in my Computer Science class. The application was to be my coursework, which makes up 20% of the AQA A-level Computer Science grade.
January was not usually the month in which my college starts pupils on the NEA (Non-Examination Assessment), however my teacher had offered that I start early due to my prior knowledge in programming. I snatched the offer, hoping I could turn this opportunity to spend hours of my time programming into something more than just my A-level coursework – I wanted to create a piece of professional software that could persist as a gem in my portfolio for years to come.
What is it?
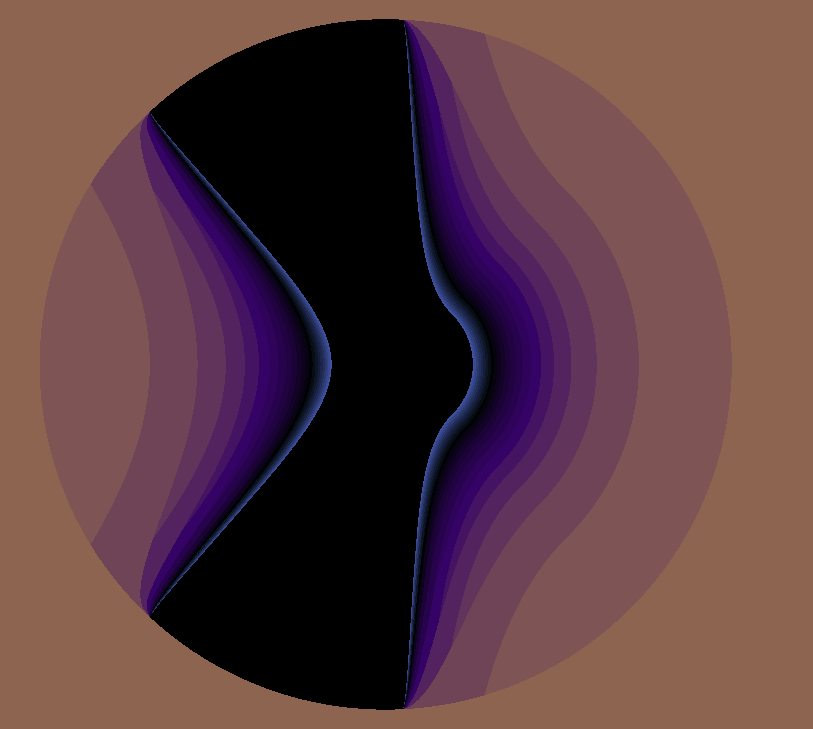
Fractal Flow is a fractal generator. Its job is to generate and export images of fractals, geometric shapes which contain a high level of detail when zooming in and often contain entire versions of themselves.
One of the most famous fractals is the Mandelbrot Set, first visualised by Benoit Mandelbrot in 1980. This infinitely detailed object is constructed over the complex plane with the formula , a deceptively simple operation for the immense complexity which is generated.

is but one of an infinite set of formulae that can be chosen to create fractals on the complex plane. These unlimited possibilities is what Fractal Flow is designed to explore. The software is fully focused on creating fractals from any formula the user can come up with – doing so with incredible performance.
Mission
From the beginning I was laser focussed on creating a product that was not only intuitive and visually attractive, but also competently engineered behind the scenes. The first step to achieving this was abandoning what was expected of me: using WinForms. I taught myself WPF (Windows Presentation Foundation) and furthermore how to use it with a professional approach. MVVM (Model View View Model) allowed for a proper separation between the user interface and the business logic and thus opened the door to code reusability.

Designing the UI
I was not happy with leaving my app with a bog-standard UI. Noticing that all the fractal generators I had tried had very tired visuals, I set about changing the expectation for how such software could look by creating a sleek, modern user interface.

This was my first time using the brilliant website Figma. I had a lot of fun designing the pages and selecting iconography and typefaces.
Rendering Kernel
The crown jewel of the application is the rendering technique I developed for it. Rather than running the computationally intense tasks in C# on the CPU, Fractal Flow hands rendering to the GPU. This allows for an enormous increase in performance (over 1000x faster in my tests).
The GPU is faster than the CPU in this field because it allows the concurrent execution of hundreds of calculations simultaneously. The colour of each pixel in these fractal images are completely independent of the other pixels in the image, so they can be treated as completely different processes to each other. This makes parallelisation really easy as each pixel can be sent as a separate job to the GPU.
To harness the power of the GPU in WPF, I used a library which provided access to OpenCL (Open Computing Language). This allowed me to provided a small piece of C code called a kernel that is to be run on the GPU. I could specify how many of these kernels are sent to the GPU and an array of arguments to be distributed between them.
This is where the clever part comes in. From the iterative formula the user specifies to generate their fractal, a line of C code representing that operation is generated. This is then implanted into the kernel to create a new program, specifically programmed to render the fractal. This approach is called metaprogramming, a technique where code writes itself.
I used this approach for technical limitations (my understanding was that using the complex number libraries in the OpenCL library kernel was unsupported so I resorted to a series of macros for my complex operations), and also because I believed that it would reap even greater computational performance over the CPU.

Proprietary Formula Parser
I created my own mathematical formula parser for this application. This was not a necessary step – reinventing the wheel for such a common process is not good practice. Regardless I made a homemade parser because: 1. It was a valuable learning process and 2. It would give me marks in my NEA 3. It allowed me total control over how the parser worked.
Developing this algorithm taught me about Dijkstra‘s Shunting Yard Algorithm (yes the same Dijkstra who invented the route finding algorithm), which converted an expression in infix notation to the Reverse Polish Notation required for execution by computers.
I also made sure my algorithm allowed for relatively natural expression. For instance it accepted notation such as ““, the terse form of “
“. I realised I could summarise token adjacency behaviour in a table:

Current State
I left Fractal Flow in a state I was relatively happy with, however there were still many features I envisioned for the application that have not made it to the application yet. For instance I initially wanted the application to be able to produce zooming videos, and have a multitude of different colouring algorithms as found in other fractal generators.
It was investigating colouring algorithms where I found a large problem with the code of Fractal Flow – an issue so large that it led to a downfall in motivation to develop the project. The problem was that many colouring algorithms require information *other* than simply the number of iterations each pixels took before it triggered the bail, such as the distance the iteration that triggered the bail “jumped” from the prior position. Implementing the inclusion of this information would require a large redesign of the render pipeline and considerable thought over how to architect a memory-efficient system.
I learnt an important lesson in discovering this flaw: to always research thoroughly absolutely everything my system might be implementing on top of what I already know it must.
There are also a few areas of the program that are unnecessary or artificially shoe-horned into the designed, with the purpose of hitting more targets on the NEA mark scheme. For example the formula parser discussed earlier, and the use of an SQL database to store fractal definition objects (I think simply storing them in files would be more reasonable).
Fractal Flow is currently over 10000 lines with over 20 classes.

GitHub README
FractalFlow
WIP – This is my A-level (Junior/Senior year equivalent) Computer Science coursework as submitted. REMEBER TO MAKE BRANCH IF WORKING ON FURTHER
Fractal Flow is a next generation application for rendering fractal images over the complex plane, with a focus on generating custom user-defined fractals.
<p align=“center”> <img src=“https://github.com/ProgramPhantom/FractalFlow/assets/49105496/bea77f82-704e-496d-a2e5-73ba33bd892d” /> </p>
Mission:
Fractal Flow aims to streamline and accelerate the process of exploring new fractal objects – beyond the Mandelbrot set. Fractal Flow combines a blazing fast rendering kernel with a UI whioh empowers rapid iteration and generation of ideas.
Architecture:
- Windows Presentation Foundation (C#)
- Model View View Model (MVVM) design principal
- MVVM implemented using Caliburn Micro
Implementation detail:
- Fractal Flow uses a meta-programming approach to achieve superior performance. The application generates an OpenCL Kernel specifically for the formula specified, which is ran on the GPU.
- The application currently also includes a renderer for the CPU, however it is highly unoptimised and unfeasibly slow, and thus will no longer be maintained.
User Interface
Features
- CPU & GPU rendering capabilities
- Create a custom fractal by specifying a formula
- Natural math expression achieved through proprietary formula parser
- Two types of fractal colouring algorithm
- Specify iterations, bail value and region on the complex plane
- Save and load proprietary .frac fractal definition file
- Save fractal image as .png
- Random colours button
- Console Window
- Fractal definition objects saved in SQL database
Started 12th Jan 2022