The inverse of a function can be found by swapping x and ys in an equation (and then rearrange back to terms of x). This has the effect of reflecting the original function in the line y = x, as you are essentially just swapping the x and y axis.

Some mates and I sat down a few weeks ago and tried to ask the question: how do we reflect in a different line, not y = x. We set out to construct a robust description of reflection, so we could get the equation of any a reflection of any function, in any other function!
We decided that we would need to find an equation to get the gradient of a line based on two other lines: one the reflectant (which can be imagined as the incident ray) and the reflector (the mirror or boundary). I set out to find this formula and here is what I found:
Variation 1
This is the second version of the formula for the gradient of reflection (the first being a method similar to this but with an unnecessary step, making it less simplified).
The aim is to have two equations:
Reflectant: y=m1x
Reflector: y=m2x
And we want to find the gradient of the line which is formed when the reflectant is reflected in the reflector. We know from physics that the angle of incidence (the angle the reflectant makes with the normal at the point of collision with the reflector) is equal to the angle of reflection:

Now we’ve got that essential aspect out of the way, let me explain how I derived the formula:
First know that we can represent a line as a complex number, 1 + im, where m is the gradient of the line we want to convert to this complex representation. So for example the line y=x can be represented as the complex number 1 + i, and the line y = -3x can be represented like 1-3i.

This works when there is 1 on the real axis, as then the y value is equal to the gradient.
Now, consider this example:
The reflector line is x = 0 (lets ignore that this is not possible in the form I said the lines would be in earlier), and the reflectant is y = -x.

Imagining the reflector line as the complex number (1-i), to get the reflected line we must get it’s complex conjugate, and then convert it back into the equation of a line. So (1-i) goes to (1+i), which is the complex number which represent the line y = x, giving us our reflected line.

Okay, so lets add getting the complex conjugate to our list of things we need to do.
Second consider the setup: Reflector: y = x, Reflectant: x=0.

Imagining again the reflectant line as the complex number (0-i) and the reflector (1+i), lets call (0-i) z1 and (1+i) z2. When you multiply together two complex numbers, you can imagine it as two properties of the complex numbers interacting:
The Argument of a complex number is the angle the line between the point and origin makes with the positive part of the real axis.
The Modulus of a complex number can be described as the distance from the number to the origin.
When you multiply two complex numbers, the resulting complex number will have a modulus that is the product of the two original numbers, and a argument that is the sum of the two original numbers.
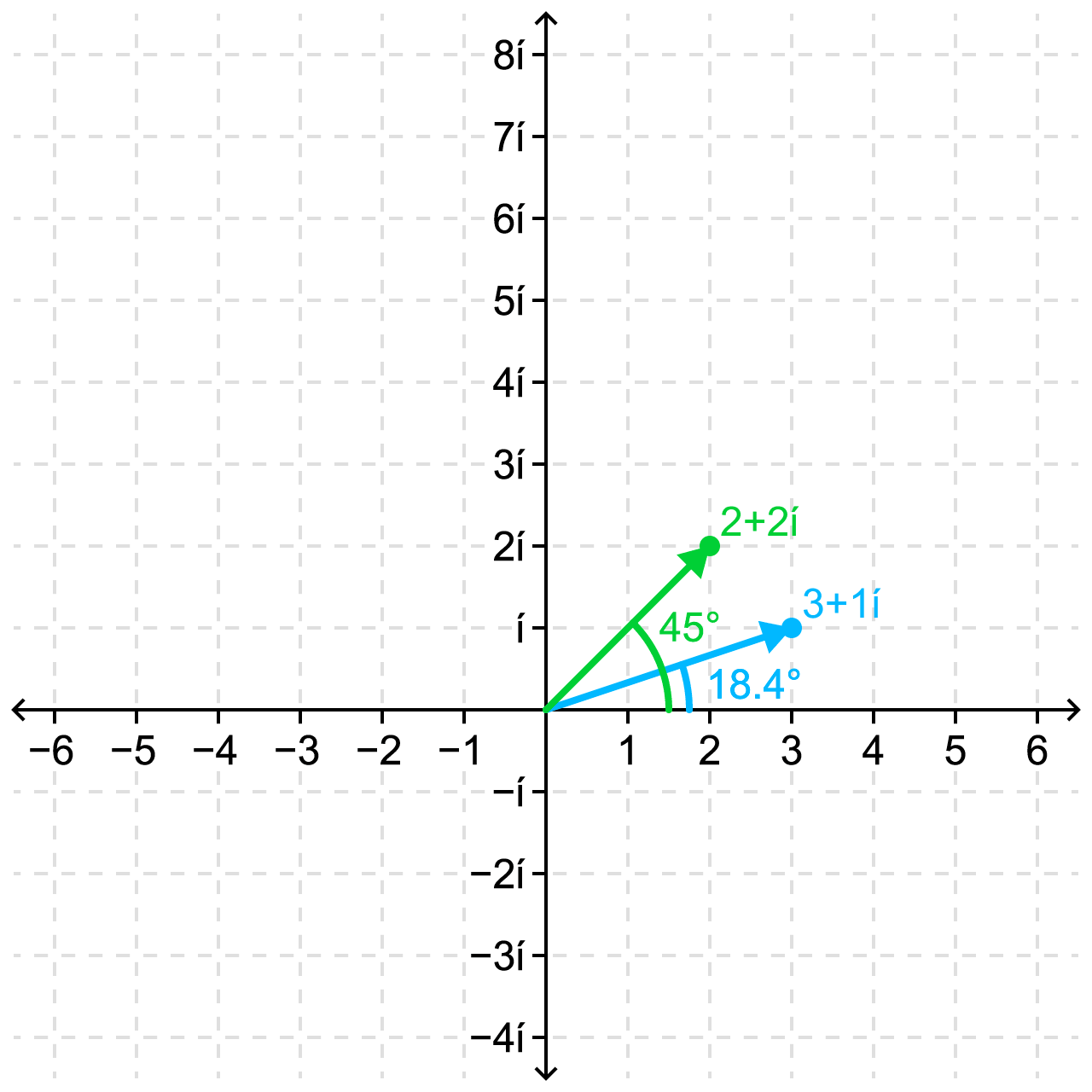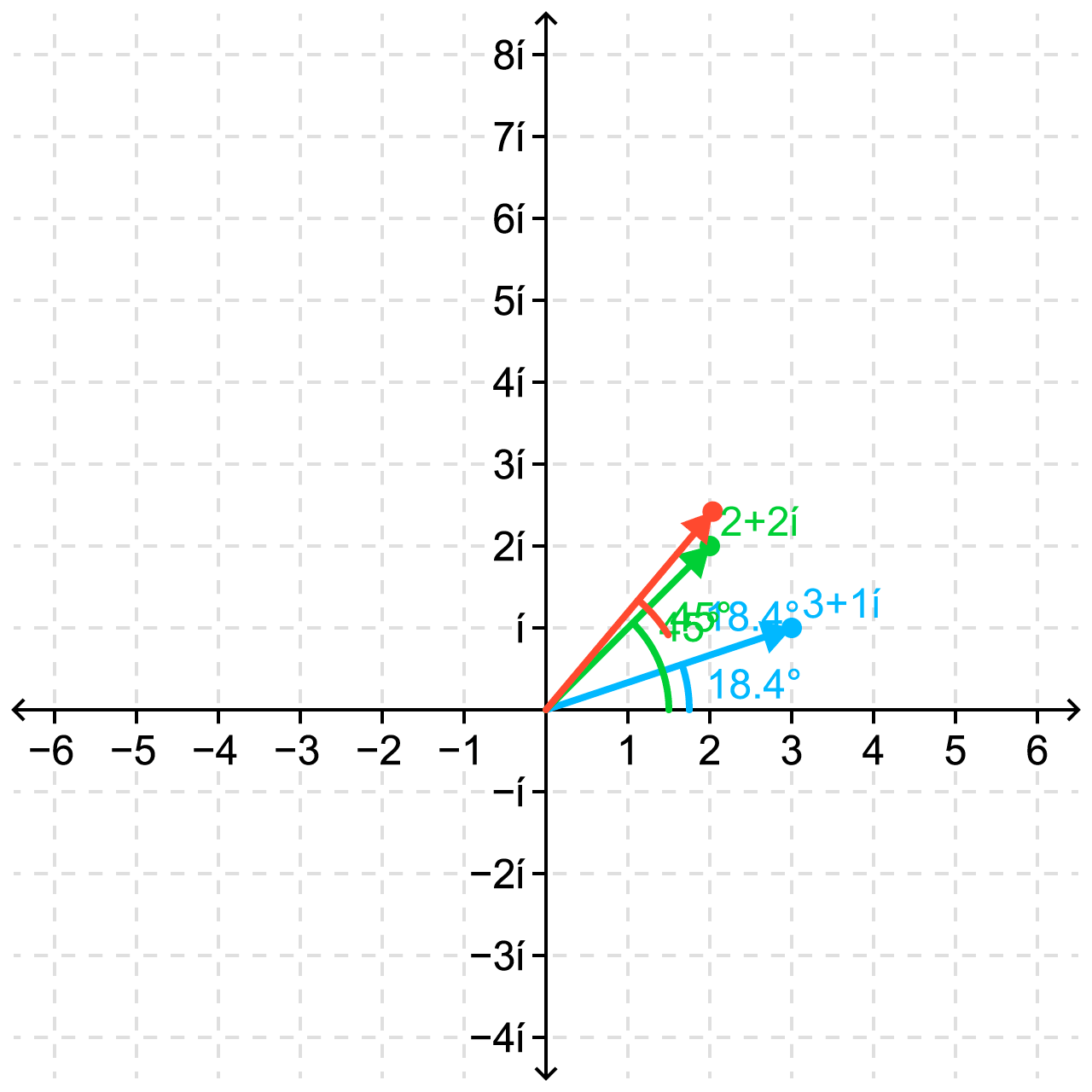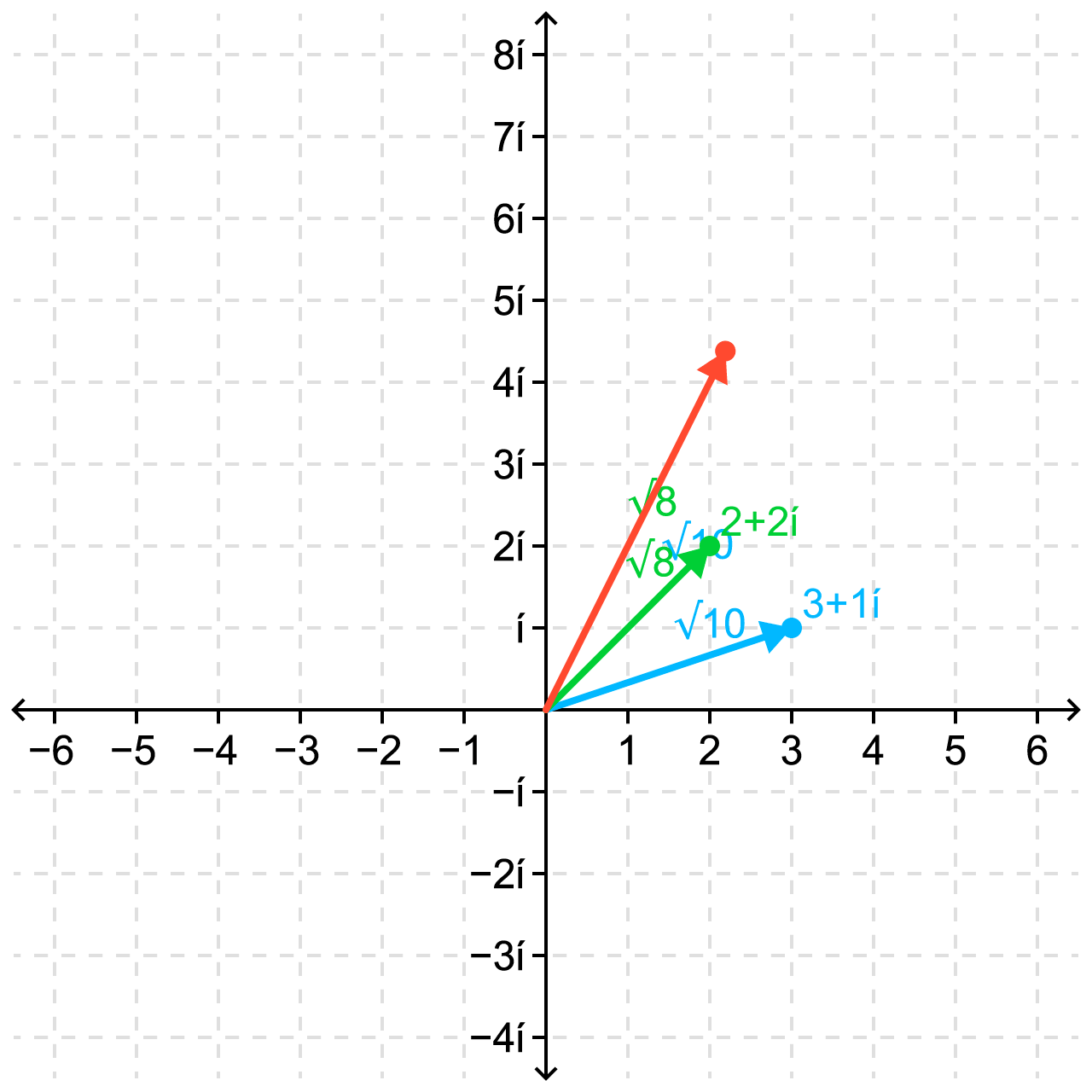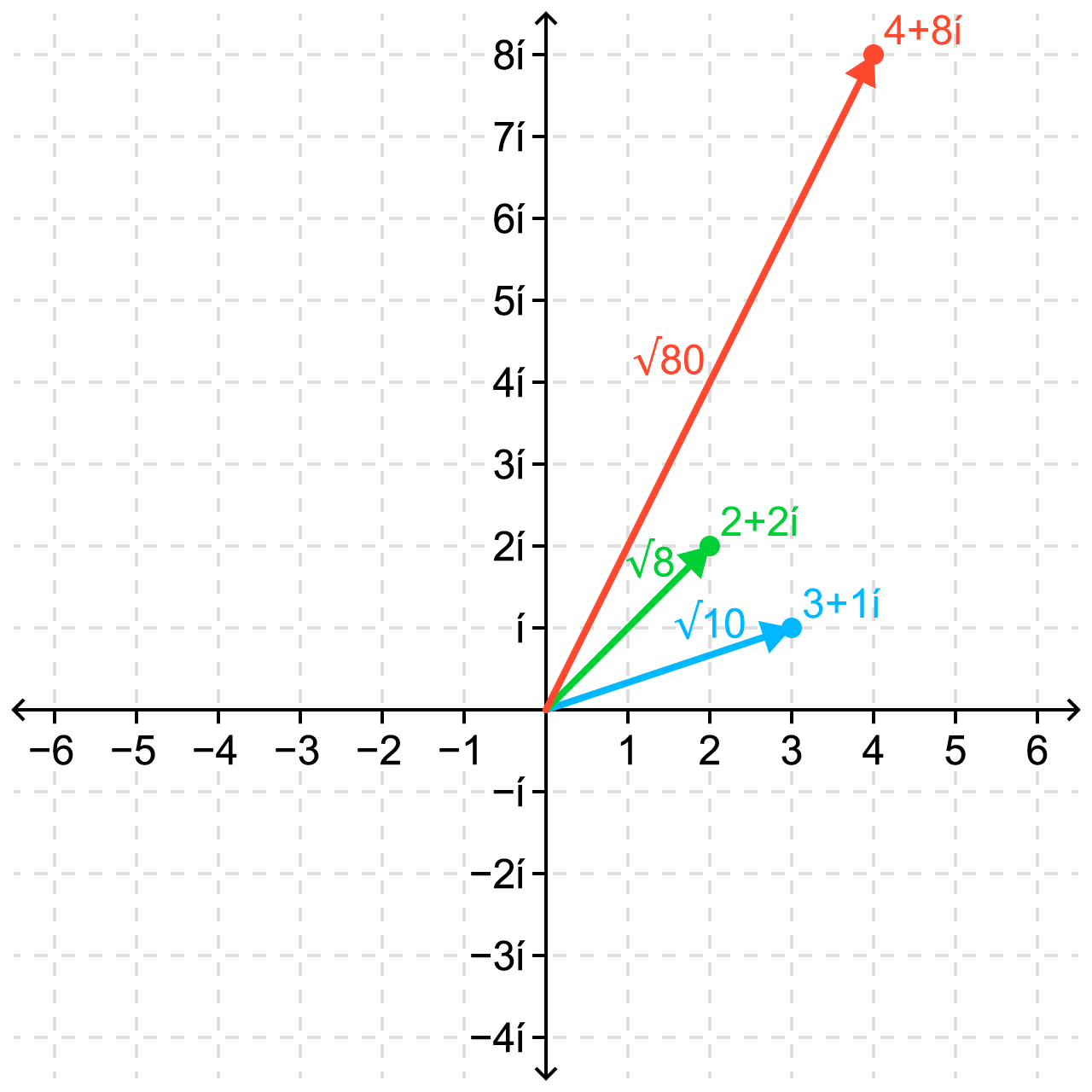
Going back to our original scenario, observe that the modulus of z2 is π/4 (45⁰) and the modulus of z1 is -π/2 (-90⁰). The line we want to get is going to be y = 0, represented by the number 1 + 0i. So to get this, we need to multiply z1 by z2 TWO TIMES, to get a number with an argument of 0 (-90 + 2 * 45 = 0).
Okay, so lets add multiplying by z2 two times as another one of the things we need to do.
This gives us the formula:
Okay, lets expand this:
We now have this complex number, but its not useful to us yet, as the real part is not equal to 1.
So if we multiply the complex number by 1 / Re (z) we will scale the entire thing so the real part is 1 and the imaginary part is whatever it lines up with.
Also at this point we can do a special trick, removing the i. Treat the imaginary part as the “y” and the real part as the “x”. This way the equation can be generalised to the Cartesian plane.
This gives us the final form of the equation:
Variation 2
There is more that can be done – a slightly different approach…
A complex number can be written in the form
Where r is the modulus of the complex number and θ is the argument of the complex number.
So if we convert our formula at the earliest step, we get this:
We can simplify this by changing the arg functions to arctan(m1 or m2) (as the real part of z1 and z2 are just 1 and the imaginary part is simply the gradient of the lines those numbers represent). We can also use indices laws to first put the power of two into the second e’s exponent, and then add the exponents of both e factors, as they have the same base. We now get this:
To go further, we must figure out how to get this formula to work on the cartesian plane, and thus must convert the formula into a complex number in the form a + bi.
To do this, we can use the mod-arg form of a complex number, so:
First, factor out i:
And see that now:
So now sub theta into the mod-arg form of the complex number:
And now we can just do what we did in the prior variation of this formula. Imagine we are scaling up the real part to 1, dragging the imaginary part along so it is the gradient of the new line. Do this by multiplying the imaginary part by 1 over the real part (dividing by real). Lets drop the i now as well:
Now you will see that this can be simplified by the trig identity tan = sin over cos, and we get the final formula!
You can play around with
Variation One: https://www.desmos.com/calculator/vtoxqqta11
and
Variation Two: https://www.desmos.com/calculator/377n9twxwl
On Desmos
Thank you for reading.
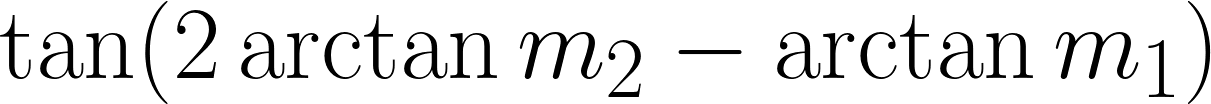


 is negative, the result will be the obtuse angle between the two vectors. So if you want the acute angle, do 180 – θ.
is negative, the result will be the obtuse angle between the two vectors. So if you want the acute angle, do 180 – θ.



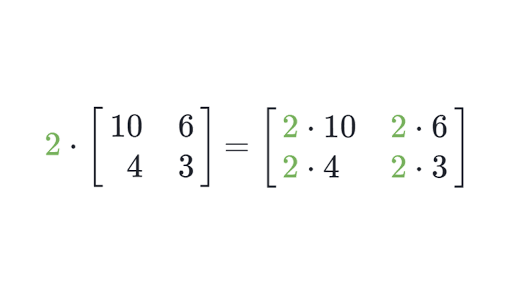




 is an enlargement sf 2 around (0, 0), meaning both basis vectors double. This of course increases the area by 4x as the distances are doubling in two directions.
is an enlargement sf 2 around (0, 0), meaning both basis vectors double. This of course increases the area by 4x as the distances are doubling in two directions.