Big Page on Matrices

What is a Matrix??

A matrix is a way of showing information efficiently. It is a rectangular array of numbers.

Matrices have two dimensions: the number of rows (usually denoted as as m) and the number of columns (denoted as n). The order of a matrix describes it’s size.

Operations on Matrices

Addition and Subtraction

Adding and subtracting matrices is really easy. Just take each element and do the required operation on the corresponding item. YES this does mean both matrices have to be of the exact same order.

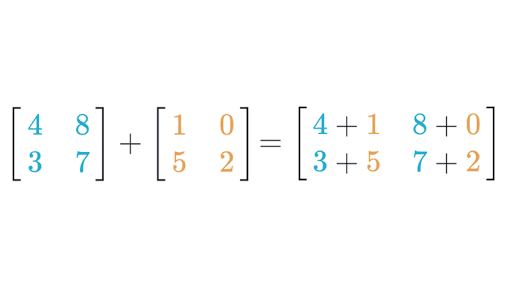
Multiplication by a scalar

Multiplying (and dividing) by a scalar is also pretty easy. Simply apply the operation to all items in the matrix and BOOM you’ve got your answer:

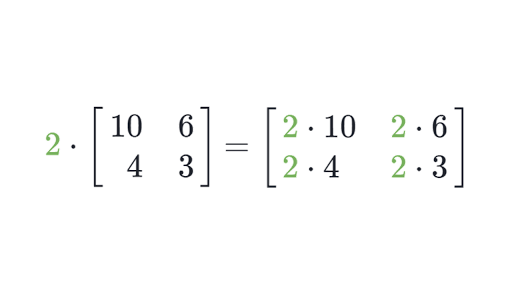
Matrix Multiplication

But what if we want to multiply two MATRICES together??! The circumstance where this is possible is if the number of columns (n) in the first matrix is exactly equal to the number of ROWS (m) in the second matrix.

When this condition has been met, this is what you do:

1. Select the first row of the first matrix
2. Select the first column of the second matrix
3. Multiply each number in the first list by the corresponding number in the second list, and add them up
4. Place the sum in the first row, first column of the output matrix.
5. Repeat the process for all combinations of rows and columns

NOTE: the position of the number outputted by the above in the output matrix is whatever row the first matrix is on (m) as the y, and whatever column the second matrix is on (n) being the x.

There is no such thing as matrix division.

Matrix multiplication is non-commutative, meaning AB ≠ BA.

Maths

---

What can a matrix be used for?

Linear Transformations

Matrices are best used to describe linear transformations. That means the map a point onto another point. This can be visualised by stretching and/or rotating a plane or space.

A two by two matrix represents a linear transformation which works on a 2D plane, three by three represents a transformation on 3D space etc…

NOTE: AS THESE TRANFORMATIONS ARE LINEAR, THE ORIGIN ALWAYS MAPS ONTO ITSELF

A vector can be mapped into the transformed version of itself by applying the matrix multiplication as shown:

The new vector is called the image.

Solving Simultaneous Equations

Due to the way matrices are multiplied together, matrices are perfect at solving systems of equations! 😁

Take this one for example:

You can separate the coefficients from the variables like so:

Then, pre-multiply the inverse of the matrix of coefficients, to get a formula giving the values of x, y and z:

Modelling

Matrices are great at modelling things in real life, such as populations.

Most questions will give you some information revolving around the total quantity of something, and how it changes from one time to another.

To solve, find 3 equations which represents this system, and solve them as simultaneous equations using the matrix method.

---

Identity Matrix

Matrices that are square have a value called the Identity Matrix. The Identity Matrix essentially acts as “1” in matrix multiplication.

You can recognise the identity matrix by the leading diagonal being 1’s and all other items being 0. This matrix does nothing.

Zero Matrix

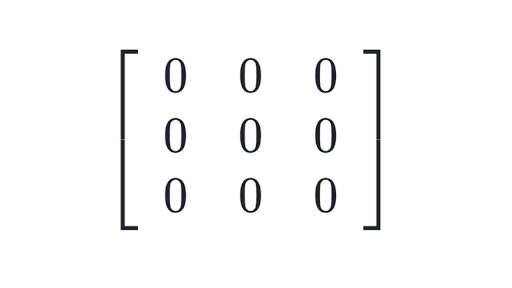
Figuring out a matrices’ transformation

To figure out what exactly a matrix is doing to the plane, simply imagine the first column and the second column of the matrix as the new position of the (1,0) and (0,1) basis vectors respectively.

---

Matrix rotation

There is a faster way to check if a matrix is rotating: if you see a matrix with signs in the pattern following (they could be the opposite sign):

It is rotating the plane (this might not be the only thing it’s doing). In the case of the matrix above, it applies a rotation counter clockwise to (x, y) by θ degrees.

---

The Determinant

The determinant is a property of a transformation vector which represents the ratio of the area (or volume) between the original plane (or space) and the transformed plane (or space). So its how much bigger the area/space gets.

For instance the matrix is an enlargement sf 2 around (0, 0), meaning both basis vectors double. This of course increases the area by 4x as the distances are doubling in two directions.

2 by 2 Determinant

You can calculate the determinant of a 2 by 2 matrix with this formula:

3 by 3 Determinant

To find the determinant of a 3 by 3 matrix:

1. Multiply one of the three numbers along the first row of the matrix by the 2 by 2 matrix left when taking out the rows and columns corresponding to that number.
2. Apply the magic signs!

3. Add them up.

---

The determinant of a matrix will go negative when the plane has been “flipped” (watch the gif to visualise what this means)

If a matrices’ determinant is 0, it means all of space has been squashed into a lower dimension

If det(A) = 0 the matrix is SINGULAR (no inverse)

If det(A) c 0 the matrix is NON-SINGULAR

You can’t have an inverse of a singular matrix because there is no way to extract area back out from a line with a linear transformation.

The Inverse of a Matrix

The inverse matrix applies the opposite transformation on the plane, undoing the first transformation:

AKA

This reads: apply the transformation of matrix A, then apply the transformation of inverse matrix A equals the matrix that represents no change. In this case, A and A^-1 can be swapped as they just do the opposite of on another.

Inverse of 2 by 2 matrix

Use this formula to get the inverse of a 2 by 2 matrix:

Inverse of 3 by 3 matrix 🥶

First off, the transpose of a matrix is found by flipping the matrix on it’s diagonal:

Here’s how to get the inverse of matrix A (any non singular 3 by 3 matrix) by hand

• Find det(A)
• Construct a matrix of minors of A, to make a 3 by 3 matrix of 2 by 2 matrices

• Get the determinant of every minor matrix to get a new 3 by 3 matrix!
• Apply the magic signs!

• Transpose the matrix of cofactors!

• Multiply by 1/det(A)

• DONE

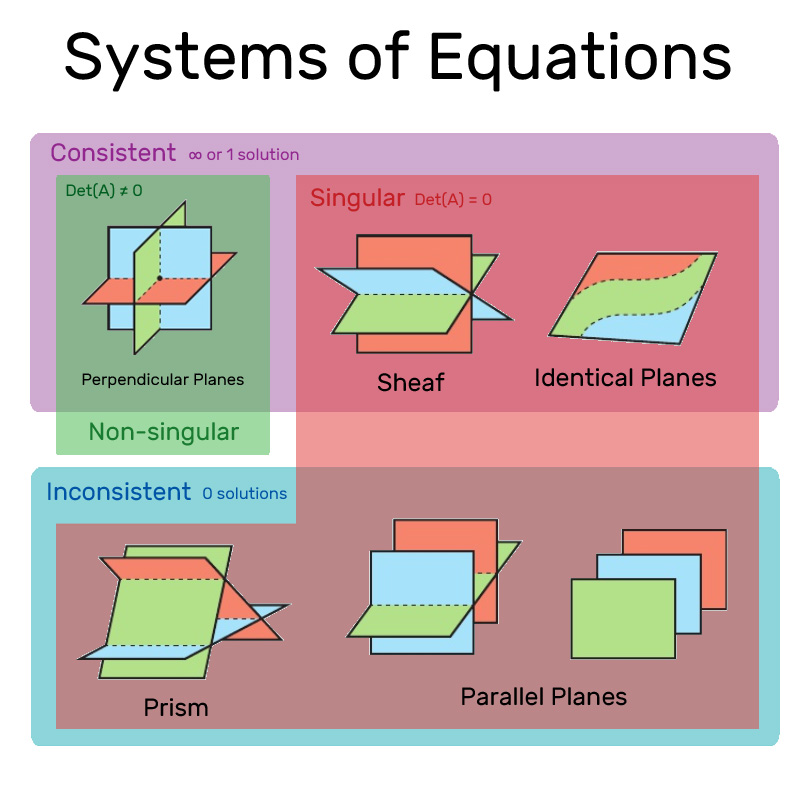
Consistent or Inconsistent?

• A matrix is consistent when the corresponding system of equations has at least one solution
• A matrix is inconsistent when the system of equations has zero solutions

This is the most common case, where there is a single set of x, y and z which satisfies all equations. The determinant here is not 0.

How to figure it out:

Invariant points and lines

An invariant point is a point unaffected by a transformation.

An invariant line is when each point on a line is transformed to another point on the same line.

	Reflections	Rotations	Enlargement
Invariant Lines	Mirror line and all lines perpendicular.	None, unless the angle = 180°, In which case all lines through (0, 0).	All lines through (0, 0).
Invariant Points	All points on mirror line.	(0, 0)	(0, 0)

To find invariant points:

Set the point (x, y) that has the transformation applied equal to the point (x, y). (So the point is the same after the transformation).

Then, expand to get some equations:

This will either give you the equation of a line – in which case there is an entire line of invariant points – or a single value for x and y, if there is only one invariant point.

To find invariant lines:

First, suppose y = mx + c is an invariant line.

Set the matrix up like this:

After this expansion, keep in mind that x’ and y’ must be on the line y = mx + c.

Now plug these equations into the y = mx + c formula!