A vector is a quantity with both direction and magnitude
Vectors can also be denoted (xi + yj + zk) and the vector variable can be called 
The way you use a vector depends on if you are treating that vector as a position vector or a direction vector.
A vector is a position vector if the vector is describing a point relative to the origin. For instance, the vector 2i + 3j on it’s own only contains information about a movement of +2 in the x dimension and +3 in the y dimension. If you go onto say this is a position vector, this number now represents an absolute position on the plane, 2 on the x and 3 on the y (and is essentially a coordinate). If it is not specified that a vector is a position vector, it is not right to link it to the corresponding coordinate on a plane.
A position vector can be denoted 
where O represents the origin and A is a vector.
Essential vector properties / operations
Magnitude of vector
One of the most important things to know about a vector is it’s length. Use Pythagoras.
Find unit vector
The unit vector essentially tells you the fundamental information about spatial direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere.
Parallel vectors
Vectors are parallel if they are scalar multiples of each other.
Vector between two vectors
To get the difference in position between two vectors, do the following:
Scalar Product
The scalar/dot product of two vectors is the sum of the products of their corresponding components.
If the dot product of two vectors equal 0, the two vectors are at 90º to each other.
The Line
Line properties
In 2D, lines are parallel or intersect. To check if lines intersect, check if they are not parallel. To check if lines are parallel, look at the direction vector for both lines, if they are linear multiples of one another, they are parallel.
In 3D, lines can be parallel, they can intersect, and can also be skew. Skew lines are when the lines do not intersect and they are not parallel. To check if lines are parallel, see if the direction vectors are linear multiples of each other. To check if lines intersect, set the lines equal to each other, and rearrange to get two equations with two unknowns. Then plug the values of λ and μ into the z row of the original equation, if this equation is true, the lines intersect. If this z equation is false (ie the LHS and RHS are different), the lines are skew.
Vector equation of a line
The straight line r in vector line notation: λ is a variable marking that the b vector is variable in magnitude, and therefore sets the direction of the line.
a is a position vector whose purpose it is to move the line away from the origin.
Cartesian equation of a line
A line in vector equation form as such:
Can be rewritten as:
This uses the aspect of the vector equation of the line secretly being 3 separate equations, and rearranges them to make λ the subject.
Angle between two lines / vectors
To get the angle between two lines, use the following formula.
Make sure to only use the direction vectors in the lines, as they are what define the direction of the line, and therefore the angle between the lines.
If the 
is negative, the result will be the obtuse angle between the two vectors. So if you want the acute angle, do 180 – θ.
The Plane
Vector equation of a plane
The vector equation of a plane looks similar to the vector equation of a line, but has another variable and another direction vector.
b and c must not be parallel.
This creates a infinite plane of values, achieved by varying lambda and mu.
Cartesian equation of a plane
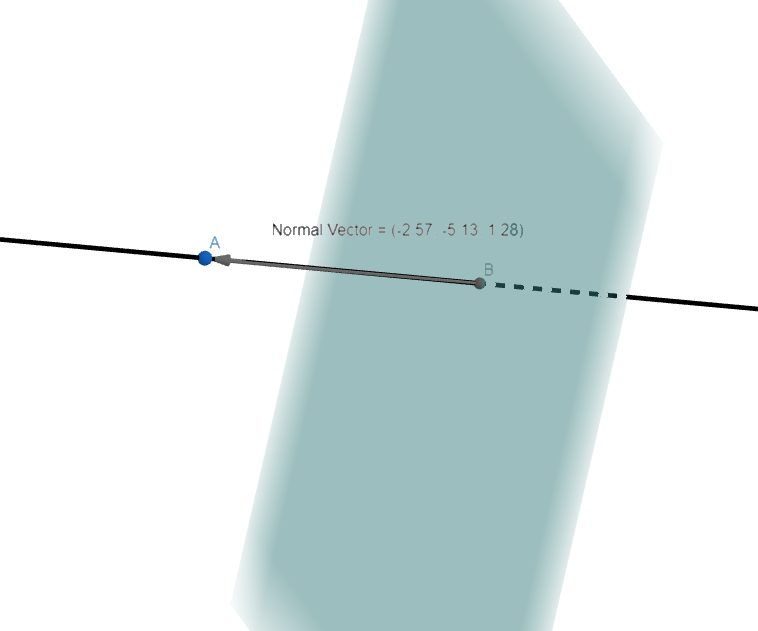
The cartesian equation of a plane harnesses the normal vector – the vector that is perpendicular to the plane.
Where
Is the normal vector to the plane.
The scalar product equation of a plane
The scalar product equation of a plane is just like the cartesian equation, but folded up a bit.
Angle between line and plane
Use the direction vector of the line and the normal vector of the plane, but note that some extra stuff has to happen once you’ve got the angle:
If you have the yellow angle, do 90 – the angle to get the acute angle between the line and the plane (purple).
If you have the blue angle, do the angle – 90 to get the acute angle between the line and the plane.
Intersect line and plane
This is the super easy one. Simply get the x, y and z formulae from the line equation, and plug those expressions into the Cartesian equation of the plane to get a value of λ.
Then plug this value into the line equation to get the position vector of the point of intersection.
